LECTURE #7 : Genetic Drift and Effective Population Size
TEXT : Hedrick, Chapter 6
What are some things that would result in a small population?
1. Limited space (limited area, limited movement between habitats, reduction of habitat, territoriality)
2. Limited resources
3. Disease
4. Environmental stochasticity (stochasticity = the inherent unpredictability of biological systems)
(floods, fires, droughts, any and all natural disasters, fluctuations in the environment seasonal changes, etc.)
RESULT OF SMALL POPULATION SIZE:
In a restricted population size - the chance of alterations in allele frequencies may have a noticeable impact on the population.
LARGE VS. SMALL POPULATIONS
LARGE
population - chance effects have a small impact.small
population - chance effects have a LARGE impact.
GENETIC DRIFT:
GENETIC DRIFT (def.) = THE CHANCE EFFECT THAT RESULTS FROM THE RANDOM SAMPLING OF GAMETES FROM GENERATION TO GENERATION.
In other words…Genetic drift is a sampling phenomenon.
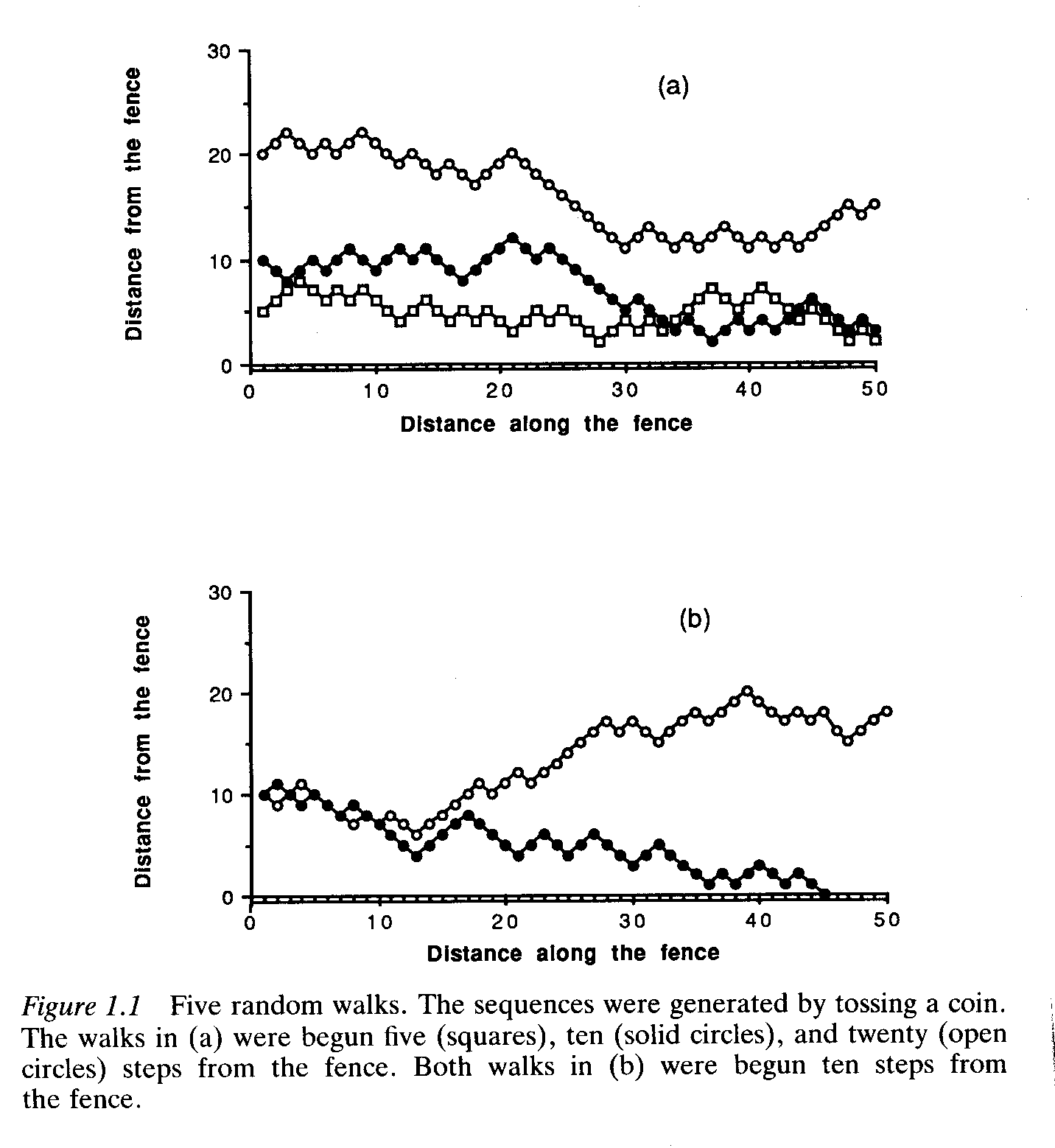
THE RANDOM WALK: UNDERSTANDING PROBABILITY
Consider yourself walking parallel to a boundary fence. At every step, you move either towards or away from the fence. You decide which direction to take after flipping a coin. If it's heads, you move towards the fence. If it's tails, you move away.
The chance of crossing the fence within the first 50 steps is greater if you begin close to the fence than if you begin very far away.

ALLELE FIXATION
If you think about genetic drift in the same way as the random walk along the fence, you can see that zero is what's known as an 'absorbing boundary' -- in other words, there's no going up from zero (if you think of this absorbing boundary as a fence, you could probably climb over it -- if it means you have NO A2 alleles left, there's no getting them back!)
REMEMBER THIS: "The ultimate fate of any sexual population lacking mechanisms to restore genetic variation would be fixation of one allele at each genetic locus throughout the genome." (Lacy, 1987)
TEST THE RANDOM WALK CONCEPT YOURSELF:
Experiment #1 - (example in book)
GIVEN: You have a diploid population of 5 individuals (10 gametes)
This is your population gene pool:
A1, A1, A1, A1, A1, A2, A2, A2, A2, A2
Step #1: Flip a coin 10 times.
Make heads = the probability of picking one of the A1 gametes
Make tails = the probability of picking one of the A2 gametes
Question : What is the frequency of your alleles after 10 flips?
(if you were lucky enough to get 0.5 A1s' and 0.5 A2s' the first time -- this is called 'beginner's luck' in gambling circles -- try it a few more times and see if you get it again!)
Experiment #2
GIVEN: You have a diploid population of 100 individuals (200 gametes)
This is your population gene pool:
100 A1 alleles
100 A2 alleles
Step #1 : Flip a coin 200 times.
Make heads = the probability of picking one of the A1 alleles
Make tails = the probability of picking one of the A2 alleles
Question : What is the frequency of your alleles after 200 flips?
*(psst…I don't really expect you to try this…BUT if you did this experiment, your frequency for A1 or A2 should range between 0.45 and 0.55 -- frequencies that are much closer to the original 0.5 A1s and 0.5 A2 frequencies you had when you started )
COMPARE THE TWO EXPERIMENTS:
What conclusions can you draw about allele frequencies and chance effects?
Expected Heterozygosity -- a way to measure the effect of genetic drift
The consequences of probability: A finite population will eventually become homozygous by chance -- (i.e. heterozygosity will approach ZER0).
HERE COMES THE MATH: (important formula to follow!)
Ht = (1 - 1/2N)tHo
Ht - this is your heterozygosity for generation t
N - this is the number of individuals in the population
Ho- this is your initial observed heterozygosity
THINKING ABOUT THE MATH:
What does the following part of the equation mean? (it is often helpful to think of a mathematical equation in verbal terms).
[1-1/2N]
By plugging any number in for N, you can see that the result will be a number less than one -- this means that expected heterozygosity will always decline and will approach zero over time at a rate dependent on the size of the population.
*IF YOU DON'T SEE THIS, GET OUT A CALCULATOR AND PLUG IN AN ASCENDING OR DESCENDING SERIES OF NUMBERS FOR N -- TRY THIS OUT AT HOME. I CANNOT ENCOURAGE YOU STRONGLY ENOUGH TO DO SO!
EXAMPLE FROM BOOK: Drosophila melanogaster and the frequency of two alleles at the brown locus.
This example uses the equation provided above and shows you how it works for a real population.
N = 10
Ho = 0.5
Ht = (1 - 1/2N)tHo
Following the heterozygosity within the population over 100 generations
H2 = (1 - 1/2(10))2(0.5) = 0.451
H3 = (1 - 1/2(10))3(0.5) = 0.428
H4 = (1 - 1/2(10))4(0.5) = 0.407
H5 = (1 - 1/2(10))5(0.5) = 0.387
H6 = (1 - 1/2(10))6(0.5) = 0.368
H7 = (1 - 1/2(10))7(0.5) = 0.349
H8 = (1 - 1/2(10))8(0.5) = 0.332
H9 = (1 - 1/2(10))9(0.5) = 0.315
H10 = (1 - 1/2(10))10(0.5) = 0.299
H100 = (1 - 1/2(10))100(0.5) = 0.00296
H1000 = (1 - 1/2(10))1000(0.5) = 0.0000000000000000000000265
RELATING HETEROZYGOSITY TO GENETIC DRIFT AND POPULATION SIZE:
In the example above…
Proportion of population that is heterozygous after 10 generations = 0.29
(0.29)10 = 2.9 individuals
Proportion of population that is heterozygous after 100 generations = 0.00296
(0.00296)10 = .0296 individuals (QUESTION: Is this possible? ANSWER: No!)
Therefore, heterozygosity in the population will probably be gone by this point…
if you try numbers until you figure out when you will lose heterozygosity because of having too few heterozygous individuals, the solution is probably somewhere around…
H31 = (1 - 1/2(10))31(0.5) = 0.1019
(.1019)10 = 1.019 individuals
…ah, one lonely heterozygote…there's still hope…
H32 = (1 - 1/2(10))32(0.5) = 0.0968
(.0968)10 = 0.968 individuals
**you will probably lose the heterozygosity in your population somewhere around 32 or more generations, although if you look at the numbers above, there is still some heterozygosity (i.e. 2.65 x 1023) in the population after 1000 generations.
SEE Example 6.3 in text (page 97 -- the Northern Elephant Seal)
THE RELATIONSHIP BETWEEN POPULATION SIZE AND HETEROZYGOSITY
The concept of the VARIABILITY and RANDOMNESS: what this means when thinking about genetic diversity:
TRY THIS AT HOME:
Experiment #1 : flip a coin ten times, record # heads and # tails
Experiment #2 : flip a coin ten times, record # heads and # tails
Experiment #3 : flip a coin ten times, record # heads and # tails
Experiment #4 : flip a coin ten times, record # heads and # tails
Experiment #5 : flip a coin ten times, record # heads and # tails
Experiment #6 : flip a coin ten times, record # heads and # tails
Experiment #7 : flip a coin ten times, record # heads and # tails
Experiment #8 : flip a coin ten times, record # heads and # tails
Experiment #9 : flip a coin ten times, record # heads and # tails
Experiment #10 : flip a coin ten times, record # heads and # tails
QUESTION: How many times did you get the same proportions?
CONSIDER THE FOLLOWING PICTURE OF RANDOM GENETIC DRIFT:
WHAT IS 'EFFECTIVE POPULATION SIZE'?
In any given population, only a proportion of the individuals will contribute offspring to the next generation.
Additionally, some individuals may produce more offspring than others.
How can this happen?
1. Mating strategies
3. other (see your notes)
Part 1: How to Determine the Effective Population Size
HERE COMES THE MATH AGAIN! (important formula to follow…)
Ne = 4NfNm/Nf + Nm
Ne - Effective population Size (i.e. the number of individuals that are actually reproducing as opposed to the total population)
Nm - this is the number of breeding males in the population
Nf - this is the number of breeding females in the population
if Nm = Nf , then Ne = N
PLEASE TRY THE ABOVE BY PLUGGING NUMBERS INTO THE ABOVE FORMULA AND PROVE IT TO YOURSELF -- also, STUDY THE FOLLOWING EXAMPLES!!!
EXAMPLE: A population of Mute swans
Say that;
N = 10 individuals in the population
Nm = 5 and
Nf = 5
then Ne = 4(5)(5)/5+5 = 100/10 = 10
(there are 10 individuals in the breeding population -- 5 males and 5 females.)
However…
IN SOME SPECIES, THE NUMBER OF BREEDING MALES AND FEMALES ARE UNEQUAL: How to use Effective Population Size and take this into account.
For example, in some social vertebrate populations, one male may mate with many females…let's consider a group of Red Deer;
N = 11 individuals
**however…there is 1 male and 10 females -- this male breeds with all of the females.
Effective Population Size then becomes the following;
Nm = 1 and
Nf = 10
then Ne = 4(1)(10)/5+1 = 40/6 = 6.66 (this is the size of the breeding population !)
PUTTING THE CONCEPTS OF GENETIC DRIFT AND EFFECTIVE EFFECTIVE POPULATION SIZE AND GENETIC DRIFT CONSIDERED TOGETHER:
Ht = (1 - 1/2 Ne)tHo
(do you notice the Ne in place of the N that used to be there in the above formula?
It's that simple!)
*loss of heterozygosity through the sampling phenomenon of genetic drift should take into account the actual size of the breeding population -- not the number of overall individuals, some of which are not contributing their genes to the next generation.
QUESTIONS TO ASK YOURSELF:
1. How important are changes in allele frequencies over time?
2. How important is variability within a population?
*Think about these questions…